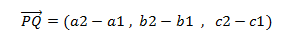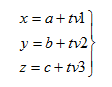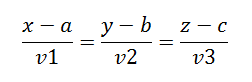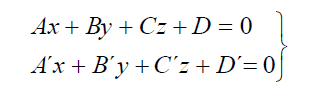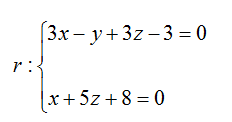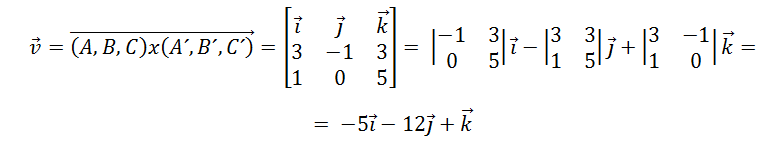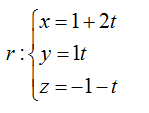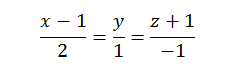CRONOGRAMA DEL CURSO CÁLCULO III

     I.         INFORMACIÓN GENERAL

1)   Denominación:	Cálculo III
2)   Facultades:	Ingeniería Civil, Ingeniería Eléctrica, Ingeniería Mecánica, Ingeniería de Sistemas e Ingeniería Industrial.
3)   Carrera:	Licenciatura en Ingeniería
4)   Semestre:	Primer Año, Segundo Semestre
5)   Código:	8322
6)   Frecuencia Semanal:	Teoría 4 horas.
7)   Créditos:	4
8)   Requisitos:	Cálculo I

CONTENIDO	TIEMPO PROBABLE	HORAS	FECHA PROBABLE DE PARCIALES
1.           Matrices y sistemas de ecuaciones lineales.	16 de agosto 10 de septiembre	16  horas	1er Parcial: Semana 13 de septiembre
2.     Determinantes, valores propios y vectores propios.		12 horas
3.     3. Cálculo Diferencial de Funciones de más de una Variable 4. Integración Múltiple	4 de octubre 22 de octubre	12 horas	3er Parcial: Semana del 2 5 de octubre
4. Funciones Vectoriales. 5. Introducción al Cálculo de Campos Vectoriales	25 de octubre 4 de diciembre	16 horas	4to Parcial: S emana del 2 9 de noviembre

       

CONTENIDO

1.VECTORES EN Â^N        

1.1        Introducción al concepto de vectores en R² y R³.

1.1.1        Definición de escalares

1.1.2        Definición de vector en el plano y en el espacio.

1.2  Representación de un vector en R²y R³.        

1.2.1        Representación de un vector por medio de segmento de recta dirigido.

1.2.2        Módulo y dirección de un vector.

1.2.3        Vectores unitarios.

1.2.4        Vectores unitarios canónicos o estándar i, j, k.

1.3  Generalización del concepto de vector a Rⁿ.

1.4  Operaciones básicas sobre vectores en R² y R³.

1.4.1        Suma y diferencia de vectores.

1.4.2        Producto de un vector por un escalar.

1.4.3        Propiedades de las operaciones básicas sobre vectores.

1.5  Producto escalar o producto punto. Proyecciones.

1.5.1        Definición y propiedades.

1.5.2        Ángulo entre dos vectores.

1.5.3        Proyección escalar y vectorial de un vector sobre otro.

1.5.3.1  Distancia de un punto a una recta.

1.6        Geometría del espacio R³

1.6.1   Ecuaciones paramétricas y simétricas de una recta.

1.6.2   Ecuación del plano.

1.7        Producto vectorial o producto cruz. Regla de la mano derecha.

1.7.1        Definición y propiedades.

1.7.2        Área de un paralelogramo.

1.7.3.   Producto vectorial mixto. Volumen de un paralelepípedo.

 2.      MATRICES Y SISTEMAS DE ECUACIONES LINEALES.    

2.1  Conceptos básicos de matrices.

2.2  Tipos de matrices: fila, columna, cuadrada, diagonal, escalar, identidad, triangular, transpuesta, simétrica y Antisimétrica.

2.3  Operaciones con matrices.

2.3.1  Igualdad de matrices.

2.3.2  Adición y sustracción de matrices.

2.3.3  Producto de un escalar por una matriz.

2.3.4  Multiplicación de matrices.

2.4  Sistemas de ecuaciones lineales:

2.4.1        Definición y notación de sistemas de ecuaciones lineales. 

2.4.2         Representación matricial

2.4.2.1  Matriz de coeficientes

2.4.2.2  Matriz aumentada

2.4.3        Sistemas de ecuaciones lineales: consistente, inconsistente, homogéneos y no homogéneos.

2.4.4        Solución de sistemas de ecuaciones lineales

2.4.4.1  Métodos de Gauss

2.4.4.2  Método de Gauss-Jordan

2.4.5        Cálculo de la matriz inversa por el método de Gauss.

2.4.6        Solución de un sistema de ecuaciones lineales usando la inversa.

2.5  Aplicaciones de ingeniería, economía, etc.

2.6  Rango de una matriz.

                                                                         

3.      DETERMINANTES, VALORES PROPIOS Y VECTORES PROPIOS. 

3.1  Determinantes de segundo y tercer orden.

3.1.1  Regla de Cramer.

3.2  Determinantes de n-ésimo orden.

3.3  Propiedades de los determinantes.

3.4  Matriz inversa.

3.4.1  Menor de una matriz.

3.4.2  Matriz de cofactores.

3.4.3  Matriz adjunta.

3.4.4  Cálculo de la inversa de una matriz por la adjunta.

3.4.5  Solución de un sistema de ecuaciones lineales usando la adjunta.

3.5  Valores propios y vectores propios.

3.5.1  Conceptos y propiedades.

3.5.2  Cálculo de valores y vectores propios.

4.      CÁLCULO DE FUNCIONES DE MÁS DE UNA VARIABLE.

4.1  Funciones de más de una variable.

4.2  Derivadas parciales.

         4.2.1 Derivada de orden superior.

4.3  Regla de la cadena para funciones de más de una variable.

4.4  Flujo de un vector.

4.5  Derivadas direccionales y gradiente.

4.6  Integrales dobles.

4.7  Integrales triples.

5.      FUNCIONES VECTORIALES.

5.1  Definición de función vectorial. Ejemplos.

5.2  Límite de una función vectorial.

5.3  La derivada de una función vectorial. Propiedades.

5.4  Vector velocidad y aceleración.

5.5  Vectores unitarios, tangentes y normales.

6.      INTRODUCCIÓN AL CÁLCULO DE CAMPOS VECTORIALES.

6.1   Definición de campos vectoriales.

6.1.1        Divergencia de un campo vectorial

6.1.2        Rotacional de un campo vectorial

 LIBRO DE TEXTO

Grossman, L. Stanley	Álgebra Lineal. Editorial Mc Graw Hill. Séptima Edición 2012.
LIBROS DE CONSULTA
1.      Larson, Ron y Otros	Cálculo. Editorial Mc Graw Hill. Novena Edición 2011.
2.      Louis, Leithold	El Cálculo. Editorial Oxford. Séptima Edición 2004.
3.      Bernard, Kolman y David    Hill	Álgebra Lineal Fundamentos y Aplicaciones, Pearson, Primera Edición, 2013.
4.      Stewart, James.	Cálculo de Varias Variable, Editorial Cengage, Sexta Edición, 2009
5.      Anton, Howard	Introducción al Álgebra Lineal. Editorial Limusa Wiley. Cuarta Edición 2009
6.      Purcell, Edwin	Cálculo. Editorial Pearson, Novena Edición 2007.
7.      Pool, David	Álgebra Lineal Una introducción Moderna.  Editorial Thomson. Segunda Edición 2007
8.      Bernard, Kolman	Álgebra Lineal. Editorial Pearson. Octava Edición 2006.
9.      James, Stewart	Cálculo Conceptos y Contextos. Editorial Thomson. Tercera Edición 2006.
10.  Nicholson, Keith	Álgebra Lineal. Editorial Mc Graw Hill. Cuarta Edición 2003.
11.  William, Gareth	Álgebra Lineal con Aplicaciones. Editorial Mc Graw Hill. Cuarta Edición 2001.

MATRICES

MATRIZ
Para designar una matriz se emplean letras mayúsculas. Cada uno de los elementos de la matriz  (aij) tiene dos subíndices. El primero  i  indica la fila a la que pertenece y el segundo  j  la columna.

Esta es una matriz de  m  filas  y  n  columnas, es decir, de dimensión  m x n.

Clasificación de matrices

Matriz fila Una matriz fila está constituida por una sola fila. Matriz columna La matriz columna tiene una sola columna Matriz rectangular Tiene distinto número de filas que de columnas, siendo su dimensión mxn. Matriz cuadrada La matriz cuadrada tiene el mismo número de filas que de columnas.          Los elementos de la forma aii constituyen la diagonal principal.              Matriz nula En una matriz nula todos los elementos son ceros. Matriz triangular superior Los elementos situados por debajo de la diagonal principal son ceros. Matriz triangular inferior Los elementos situados por encima de la diagonal principal son ceros. Matriz diagonal Todos los elementos situados por encima y por debajo de la diagonal principal son nulos. Matriz escalar Es una matriz diagonal en la que los elementos de la diagonal principal son iguales. Matriz identidad o unidad Es una matriz diagonal en la que los elementos de la diagonal principal son iguales a 1. Matriz traspuesta Se llama matriz traspuesta a la matriz que se obtiene cambiando ordenadamente  las filas por las columnas

 

MÓDULO 1

VECTORES EN R^N

Vector es un término que deriva de un vocablo latino y que significa “que conduce”. Un vector es un agente que transporte algo de un lugar a otro. Su significado, de todas formas, varía de acuerdo al contexto.

Los vectores se representan por medio de flechas y cada vector posee una características.

   CARACTERÍSTICAS DE UN VECTOR

   - Origen o Punto de Aplicación: es el punto exacto sobre el que actúa el vector.

   - Módulo: es la longitud o tamaño del vector. Para saber el módulo de un vector es necesario conocer el punto inicial y final del vector (origen y extremo). Para calcular el módulo se mide desde el origen hasta el extremo.

   - Dirección : viene dada por la orientación en el espacio de la recta que lo contiene. La recta que contiene el vector es su dirección, pero también es el ángulo que tiene el vector con respecto al eje de referencia. Si el eje de referencia es horizontal, el ángulo que forma el vector, con la horizontal, será la dirección.

   - Sentido : se indica mediante una punta de flecha situada en el extremo del vector, indicando hacia que lado se dirige el vector.

   A veces la combinación de la dirección y sentido se llama Orientación.

   Generalmente los vectores tienen una letra en el origen y otra en el extremo, que dan nombre al vector, por ejemplo Va-b, vector ab, o simplemente AB (con una flecha encima de las letras para identificar que es un vector).

En este módulo emplearemos “vectores” en referencia a los elementos de cualquier punto de  Rⁿ.  En R¹ = R el vector es un punto, que llamamos escalar.  En R² el vector es de la forma (x₁, x₂) y en R³ el vector es de la forma (x₁, x₂, x₃).

VECTORES EN R² 

Los vectores en R² son aquellos que están ubicados en un plano cartesiano de ejes X e Y

Un vector es aquel que tiene un inicio (X0; Y0) y un fin (X1; Y1), lo cual, que determina su sentido en el plano.

COORDENADAS DE UN VECTOR EN EL PLANO

Si las coordenadas de A y B son:

Las coordenadas o componentes del vector  son las coordenadas del extremo menos las coordenadas del origen.

MÓDULO O MAGNITUD DE UN VECTOR

Si tenemos las componentes de un vector:

Ejemplo

PRODUCTO ESCALAR 

El producto escalar es una multiplicación entre dos vectores que da como resultado un escalar.

Para vectores expresados en coordenadas cartesianas el producto escalar se realiza multiplicando cada coordenada por la misma coordenada en el otro vector y luego sumando los resultados.

A = (x₁,y₁)  B =(x₂,y₂)  entonces el producto escalar o punto es A.B = x₁.y₁ + x₂.y₂

El ángulo que forman dos vectores  y viene dado por la expresión:

VECTOR UNITARIO

Los vectores unitarios tienen de módulo la unidad.

Proyección de un vector sobre otro vector

Proyectar un vector sobre otro es encontrar el vector que tiene la misma dirección que el vector que recibe la proyección, pero su longitud depende del vector que se proyecta:

Es como una sombra:

El vector A se esta proyectando sobre B y el resultado es el vector verde.

El vector proyección es resultado de multiplicar el vector   B por un escalar, en el dibujo la proyección es mas pequeña que el vector que recibe la proyección, pero puede darse el caso de que la proyección sea mas larga que el vector que la recibe, sin embargo, no deja de ser producto de un escalar por el vector, ya que tiene la misma dirección.

Ejemplo

OPERACIONES 

1. la suma de dos vectores se define por: sean a y b vectores en R², entonces  a + b = (a₁, a₂)  +  (b₁, b₂) = (a₁ + b₁, a₂ + b₂).

2. el producto de un escalar por un vector se define por: sea α Є R  y a un vector en R² , entonces  αa = α(a₁, a₂) = (α a₁, α a₂). 

Observa que si  a = (a₁, a₂)   y   b = (b₁, b₂),  entonces la  suma  de  los  vectores

 a + b = (a₁, a₂)  +  (b₁, b₂) = (a₁ + b₁, a₂ + b₂).  El cual se obtiene trasladando la representación de los vectores a y b.  De manera, que se puede obtener  a + b dibujando un paralelogramo.  A esta regla de suma se le llama la regla del paralelogramo.

VECTORES EN R³

Un sistema de coordenadas tridimensional se construye trazando un eje Z, perpendicular en el origen de coordenadas a los ejes X e Y.

Cada punto viene determinado por tres coordenadas P(x, y, z).

COMPONENTES DE UN VECTOR EN EL ESPACIO

Si las coordenadas de A y B son: A(x₁, y₁, z₁) y B(x₂, y₂, z₂) Las coordenadas o componentes del vector  son las coordenadas del extremo menos las coordenadas del origen.



Determinar la componentes de los vectores que se pueden trazar en el triángulo de vértices A(−3, 4, 0), B(3, 6, 3) y C(−1, 2, 1).

OPERACIONES

1. la   suma   de   vectores   se   define   por:   sean   a, b  Є  R³,   entonces a + b = (a₁, a_2, a₃)  +  (b₁, b_2, b₃) = (a₁ + b₁, a₂ + b_2, a₃ + b₃).

2. el producto de un vector por un escalar se define por: sea α Є R  y a un vector en R³ , entonces  αa = α(a₁, a_2, a₃) = (α a₁, α a_2, αa₃). 

Los vectores a y b se llaman ortogonales si su producto interno es igual a cero.

Ángulo entre vectores.

Ángulo entre dos vectores, trazados de un punto, se llama el ángulo más corto al cual hay que girar uno de los vectores alrededor de su inicio hasta la posición de co-dirección con el otro vector.
El coseno del ángulo entre vectores equivale al producto escalar de dos vectores dividido en el producto de módulos de estos vectores.

Fórmula de calculo del ángulo entre vectores

cos α =	a.b
	|a|·|b|

Producto vectorial de vectores.

Se llama producto vectorial o producto cruz de vectores a  y b el vector c

, cuya longitud numéricamente equivale al área del paralelogramo constituido en vectores 

a  y  b, perpendicular al plano de estos vectores y dirigido de tal manera que la revolución mínima del a hacia b en torno al vector c se haga de la derecha a la izquierda, si verlo del final del vector c

.
Producto vectorial 

a = {x₁; y₁; z₁}   y  b = {x₂; y₂; z₂}

  en el sistema cartesiano de coordenadas – es un vector, cuyo valor se puede calcular, utilizando las fórmulas siguientes: 

a × b =	i	j	k	= i(y1z2 - z1y2) - j(x1z2 - z1x2) + k(x1y2 - y1x2)
	x1	y1	z1
	x2	y2	z2

Notas:

1. El vector cero tiene magnitud cero.  Como el punto inicial y el punto terminal coinciden, se dice que el vector no tiene dirección.

2. Como la línea recta es la distancia más corta entre dos puntos, se dice que: ║a + b║ ≤ ║a║ + ║b║.

3. Ejemplo para discusión:  Sean a = (1, 5)  y b = (3, 1).  Compara  ║a + b║  y  ║a║ + ║b║.

Definición:  Sean   a   y   b  vectores  en  Rⁿ,  donde   a = (a₁, a₂, a₃, …, a_n)   y  b = (b₁, b₂, b₃, …, b_n).  La distancia entre a y b  representada por d(a, b) está definida por:

Ejercicios:

1. Halla el producto interno a ∙ b de:

a) a = (3, -5, 2)  y  b = (4, 1,  -2)

b) a = (1, -8, 0, 5)  y  b = (3, 6, 4, 0)

c) a = (3, -1)  y  b = (2, 4)

2. Halla el valor de k para que los vectores a = (1, k, -3)  y  b = (2, -5, 4) sean vectores ortogonales.
3. Halla la norma de los siguientes vectores:

a) (2, -7)

b) (3, -12, -4)

2. Determina el valor de k tal que ║a║ = √39  si a = (1, k, -2, 5).

3. Un vector unitario a es un vector cuya norma (longitud o magnitud) es 1.  Verifica si el vector  es un vector unitario.
4. Halla la distancia entre:

a. (1, 5)  y  (1, 1) en R²

b. (3, 4, 5)  y  (2, 3, 5) en R³

c. (-2, -1, 2)  y  (-5, 1, 2) en R³

5. Halla el valor de k tal que d(a, b) = 6 si a = (2, k, 1, -4)  y  b = (3, -1, 6, -3).

APLICACIONES DEL PRODUCTO CRUZ

     

*   Producto mixto de tres vectores.

  ,  .

ECUACIÓN DE LA RECTA

La ecuación de la recta, al igual que en el plano, viene determinada por:
– un punto (P) y un vector (v) : P (a, b, c) , v = (v1,v2,v3)
– o dos puntos: P (a1,b1,c1) y Q (a2,b2,c2), de los cuales para escribir la ecuación de la recta elegiríamos uno de ellos y el vector que determinan:

A partir de este momento, ya estamos en condiciones de dar a conocer las distintas formas en que nos podemos encontrar las ecuaciones de una recta:
Ecuación vectorial de la recta:

Si escribimos por separado cada una de las componentes obtenemos las ecuaciones paramétricas:
Despejando t de cada uno de las ecuaciones anteriores e igualando obtenemos la ecuación en forma continua de la recta:

Si igualamos dos a dos las expresiones anteriores (por ejemplo la primera con la segunda, y la primera con la última) obtenemos dos ecuaciones que llamamos ecuaciones cartesianas o implícitas de la recta:

A partir de estas dos ecuaciones podemos obtener el vector director (v) de la recta mediante el producto vectorial de (A,B,C) x (A´, B´,C´), por ejemplo:

Ejemplo 1: Sea la siguiente recta r dada en forma implícita:
De tal forma que (A, B, C) = (3, -1, 3) y (A´, B´,C´) = (1, 0, 5), entonces el vector director de la recta será:

Por tanto el vector director de nuestra recta es v = (-5, -12, 1). Para obtener un punto de la recta, podemos elegir cualquier valor para x, y y z que cumpla las ecuaciones anteriores. Otra forma para obtener un punto (que no sea probando….) es resolver el sistema formado por las dos ecuaciones anteriores; este sistema es un sistema compatible indeterminado, por tanto se resolverá en función de una de ellas. Sea z = t, entonces las soluciones vendrían dadas en función de t:
x = -8 -5t, y = -27 -12t, z = t

Si t = 0, obtenemos el siguiente punto de la recta P (-8,-27,0).
Una vez que ya hemos calculado un punto y un vector de nuestra recta podemos escribir la ecuación de la recta de cualquiera de las formas que hemos visto anteriormente.

Para finalizar, vamos a realizar un ejemplo de todo lo que hemos visto:

Ejemplo 2: Sean P (1,0,-1) y Q ( 3,1, -2 ) dos puntos del plano, escribe las ecuaciones de la rectas de todas la formas posibles.
En primer lugar, tenemos que calcular el vector director de la recta:
v = ( 3-1, 1-0, -2-(-1) )= (2,1,-1)

Una vez que hemos obtenido el vector, elegimos uno de los puntos y podemos escribir la primera ecuación.

Ecuación vectorial: (x,y,z) = (1,0,-1) + t (2,1,-1)

Separando cada una de las coordenadas:

Ecuaciones paramétricas:

Despejando la t en cada una de las ecuaciones.

Ecuación continua:

Por último, igualando las ecuaciones:

Ecuaciones implícitas:

Una vez que ya sabemos escribir la ecuación de la recta en cualquiera de sus formas, podemos estudiar la posición relativa de dos rectas en el espacio, siendo la forma más fácil para realizar esta tarea escribiendo las ecuaciones cartesianas de cada una de lasa rectas.